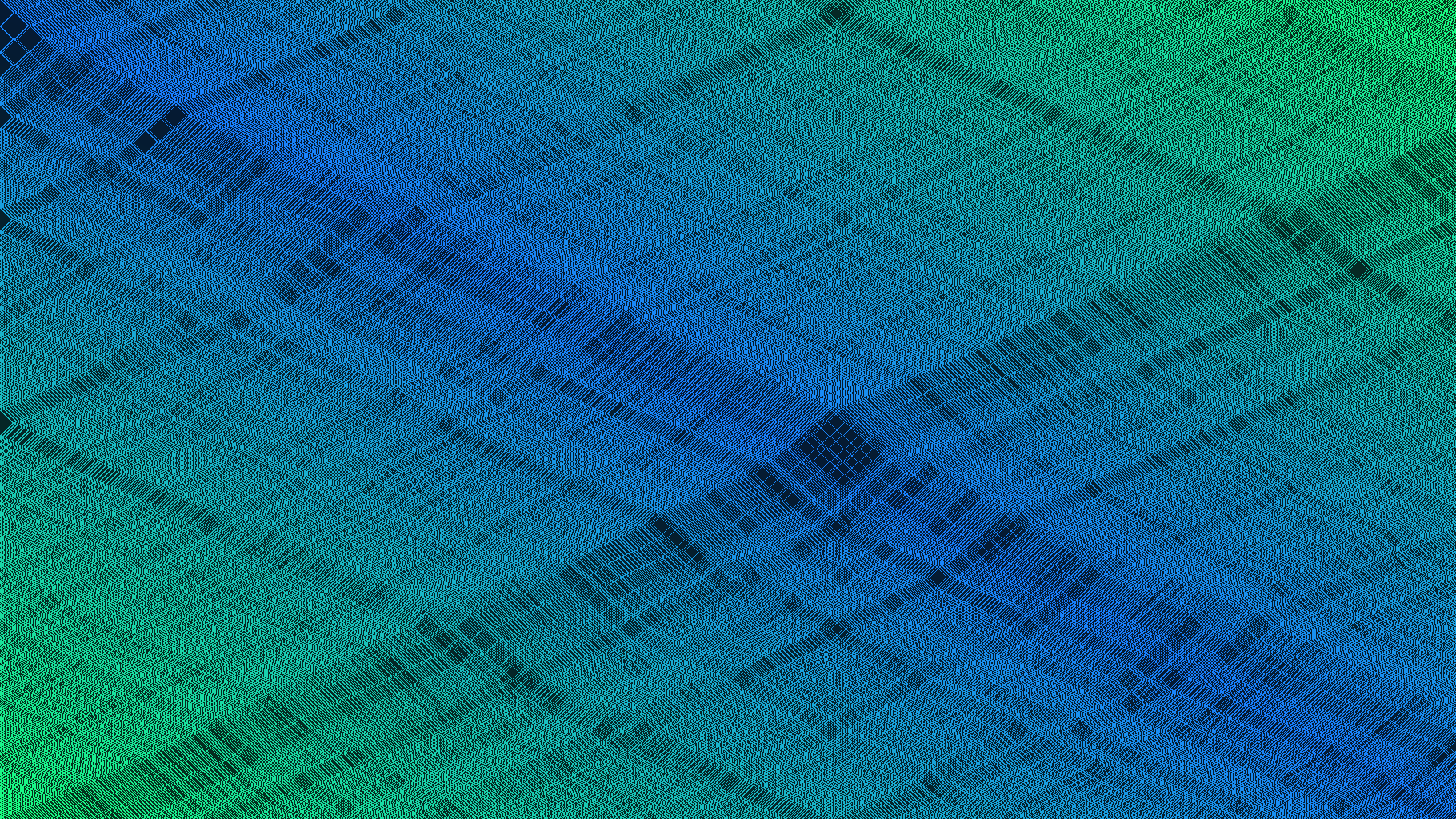
This is a reimplementation of my Bitbanging 1D Reversible Automata in WGSL so that it runs on GPUs inside a computation shader. If you are not familiar with 1D automata or bitbanging techniques then please see the original article.
WebGPU is still not available on some browsers at the time of
writing. On my Linux machine I had to set
--enable-unsafe-webgpu --enable-features=Vulkan on
Chromium to enable it. However it worked out-of-the-box with Chrome
on my phone and ancient Mac Book Air.
I’ve included some screen-shots throughout the article if you can’t get it work.
Automata viewer
Value:
If you find a particular rule doesn’t produce interesting output then try dragging the seed value to a negative value. This will populate all of the starting bit fields instead of just one.
You can find the JavaScript source here and the WGSL source here. In addition you can just open your browser’s developer console and get the files there. I didn’t use an build tools, it’s just vanilla JS.
WebGPU background
For some time I have wanted to embed the original automata viewer in my website. The original is written in C, so I thought I would try compiling it to WASM, but this wasn’t very fun.
At the same time I have been interested in learning to do something on the GPU and even if the GPU is not particularly well suited to the calculations involved it should be plenty fast enough.
Originally I tried using WebGL, but after some research I couldn’t see a way to perform the calculation in a vertex or fragment shader without multiple render calls. It may very well be possible, but it’s not obvious how to use the result of a previous calculation on a vertex or fragment without multiple stages to a pipeline.

WebGPU on the other hand has computation shaders which are perfectly suited to this type of calculation. It’s very new so I’d preferred to have steered clear of it, but it seemed to be the path of least resistance and by far the most interesting.
Probably I could get JavaScript to go fast enough to do the calculation while dealing with 1D automata. However using WebGPU paves the way for multi-dimensional automata or just displaying 1D automata in 3D.
WebGPU has its own Rust flavoured shader language that is called WGSL due to some drama with Apple and perhaps other reasons. It’s tempting to talk about this, but it’s a waste of time for both me and you. The language itself though seems pretty good although I don’t have much to base this upon.
I learnt enough about WebGPU to make this from WebGPU Fundamentals, the WebGPU specification and the WGSL spec. I also found Compute Toys useful and noticed that someone had already uploaded a 1D automata albeit not a reversible one.
WGSL automata implementation
I didn’t think I would be able to achieve quite the same result as my original implementation. Indeed only 32-bit ints are supported by WebGPU and there is no vectorisation. However none of that is needed on GPU and we can still do bit banging.
I don’t know if GPUs are limited in terms of integer arithmetic compared to floating point, but it makes no difference here. I’d have to line up more automata than could be displayed for performance to be an issue.

Below is the compute shader which calculates the next value for each automaton 16 x 32 automata at a time. There are 32 bits in an integer and the work group size is 16 by default. Meaning that the GPU will do 16 u32 computations in parallel.
Most GPUs can do at least 64 computations in parallel, but it is a bit pointless because we run out of pixels. We could write the automata activations to a much larger texture and sample multiple texels for each pixel, but I suspect it wouldn’t be all that interesting.
override stride: u32 = 16;
struct Params {
width: u32,
height: u32,
rule: u32,
reversible: u32,
zoom: u32,
};
@group(0) @binding(0) var<storage, read_write> cells: array<u32>;
@group(0) @binding(1) var<uniform> params: Params;
// Take bit n of m and if it is 1 return all 1s, if 0 return all 0s
@must_use fn bit_to_max(m: u32, n: u32) -> u32 {
let z: u32 = 0;
return ((m >> n) & 1) * ~z;
}
@compute @workgroup_size(stride) fn cmp(
@builtin(global_invocation_id) id: vec3u
) {
let rule = params.rule;
let i = id.x;
let cols = stride;
let rows = arrayLength(&cells) / cols;
// Wrap the u32 bitfields; if we are on the first or last index
let left_i = select(i - 1, cols - 1, i == 0);
let right_i = select(i + 1, 0, i == cols - 1);
// The cells before the current ones, used for reversible automata
var prev: u32 = 0;
for (var j: u32 = 1; j < rows; j++) {
let row_off = (j - 1) * cols;
let center = cells[row_off + i];
// move the cell-bits on the left and right into the center
// the bits at the edge are taken from the neighboring bitfields
let left = (center >> 1) | (cells[row_off + left_i ] << 31);
let right = (center << 1) | (cells[row_off + right_i] >> 31);
var result: u32 = 0;
// for each of the 8 3-bit patterns...
for (var k: u32 = 0; k < 8; k++) {
// is the cell (de)activated for this pattern?
let on = bit_to_max(rule, k);
// check if the left, center and right cell-bits match the pattern
// it's useful to remember that we are working on 32 cells at once
let l = ~(bit_to_max(k, 2) ^ left);
let c = ~(bit_to_max(k, 1) ^ center);
let r = ~(bit_to_max(k, 0) ^ right);
// set cell-bits to active if pattern is active and left,
// right and center cell-bits all matched
result |= l & c & r & on;
}
// for reversible automata...
result ^= prev;
cells[j * cols + i] = result;
workgroupBarrier();
prev = select(center, 0, params.reversible == 0);
}
}
The automata are drawn to the screen with a vertex and pixel shader combination. The colour gradient in the background is the result of the vertex colours being blended together. I didn’t start out with the intention of there being a gradient, but putting colours on the vertices was in the tutorial and I kept it.
struct Verts {
@builtin(position) pos: vec4f,
@location(0) color: vec4f,
};
@vertex fn vs(@builtin(vertex_index) i : u32) -> Verts {
let pos = array(
vec2f(-1, 1),
vec2f(-1,-1),
vec2f( 1,-1),
vec2f(-1, 1),
vec2f( 1, 1),
vec2f( 1,-1),
);
let col = array(
vec4f(0.1, 0.5, 1, 1),
vec4f(0.1, 1, 0.5, 1),
vec4f(0.1, 0.5, 1, 1),
);
return Verts(vec4f(pos[i], 0.0, 1.0), col[i % 3]);
}
@fragment fn fs(verts: Verts) -> @location(0) vec4f {
let fields = stride;
let cols = (32 * fields) / params.zoom;
let col_width = f32(params.height) / f32(cols);
let rows = (arrayLength(&cells) / fields) / params.zoom;
let row_height = f32(params.width) / f32(rows);
let i_off = ((32 * fields) - cols) / 2;
// get the cell's column index
let i = u32(floor(verts.pos.y / col_width)) + i_off;
// get the field index; i / 32
let f = i >> 5;
// get the bit index; i % 32
let b = 31 - (i & 31);
let j = u32(floor(verts.pos.x / row_height));
let a = 0.2 + 0.8 * f32(((cells[j * fields + f]) >> b) & 1);
return a * verts.color;
}The vertex shader positions the vertices into a rectangle made out of two triangles. Each fragment then gets a color value that is the result of interpolating between the nearest vertices to where the fragment was located on a triangle.

The automata is drawn by changing the alpha value for each fragment depending whether it falls inside an active cell. When the number of fragments equal the number of cells, then it is one cell per fragment and therefor it is one bit per cell.
Conclusion
I am excited to get something working with WebGPU and while it is complicated to get computation shaders running, I think there is a lot of potential there. When I get chance I’d like to look into higher dimensional automata and how these could be computed and displayed with WebGPU. I seem to remember that adding dimensions makes finding interesting rules far more difficult, but it would be cool to see something in 3D.